For a right angle, (rt), triangle with short sides of length a and b and a long side of
length c,
c2
= a2
+ b2
For many, the theorem is not obvious and proof is needed. The earliest known attempt
to show the truth of the theorem may have occurred as early as the
18th century BC.
Here we provide a demonstration of its truth by showing that all possible rt triangle
shapes have sides that satisfy the theorem.
This is done by constructing all rt triangle shapes within and touching the Unit
Circle, a circle with radius 1.
A short side
a is placed on the x-axis with one of its ends at the origin.
The other short side,
b,
begins at the end of
a that is away from the origin and
from there ascends or descends parallel to the y-axis until it intersects the Unit
Circle.
The long side is drawn from that intersection to join with the side
a at the origin.
When the length of the side
a on the x-axis becomes very
much less than 1, the angle between side
c and the
x-axis, the base angle, becomes
large and approaches 90
o.
As the
length of
a
approaches the value 1, the base angle becomes small and approaches
0
o.
This range of angle provides
for drawing all possible rt triangle shapes and all such triangles have their long
side
c of length equal to the radius of the circle.
Further, the set of points with coordinates x, y that satisfy
x
2+y
2
=1 all lie on a circle with radius 1.
The family of all possible rt triangles all have short sides, one of which coincides in length with the
x coordinate of a point on the Unit Circle and the other of which coincides in length
with that point's y coordinate.
For examples, hover your mouse over any of the sixteen base angles
listed below.
For each base angle chosen, a graph with the corresponding inscribed
triangle will be drawn. The graphs show the base angle of the chosen triangle, the x, y coordinates of the triangle's vertex on
the Unit Circle and the squares of those coordinates.
The Sine and Cosine functions
(Note.
In mathematics, all fundamental trigonometric identities are proved using the Pythagorean theorem.)
Closely related to the Unit Circle and the theorem of Pythagoras are the two fundamental
trigonometric functions, the sine of an angle, and the cosine of an angle.
For any of our family of inscribed triangles, the length of its short side that
lies on the x-axis is taken as the value of the cosine of the base angle.
Similarly, the length of the short side that is parallel to the y-axis provides
the sine of the base angle.
In terms of the points around the Unit Circle,
their x, y coordinates correspond to the cosine and sine of the angle between the
side c and the x-axis, the base angle.
That angle is considered
herein to increase from the value 0.0o
when c is aligned with the positive x-axis through positive
values as c is rotated counter clockwise and to decrease
through negative values as c is rotated clockwise from
alignment with the positive x-axis.
(The direction of rotation and initial
alignment that are assumed here are not fully standardized among the professions.)
The following graph shows two full cycles of the sine and cosine values versus the
angle of rotation.
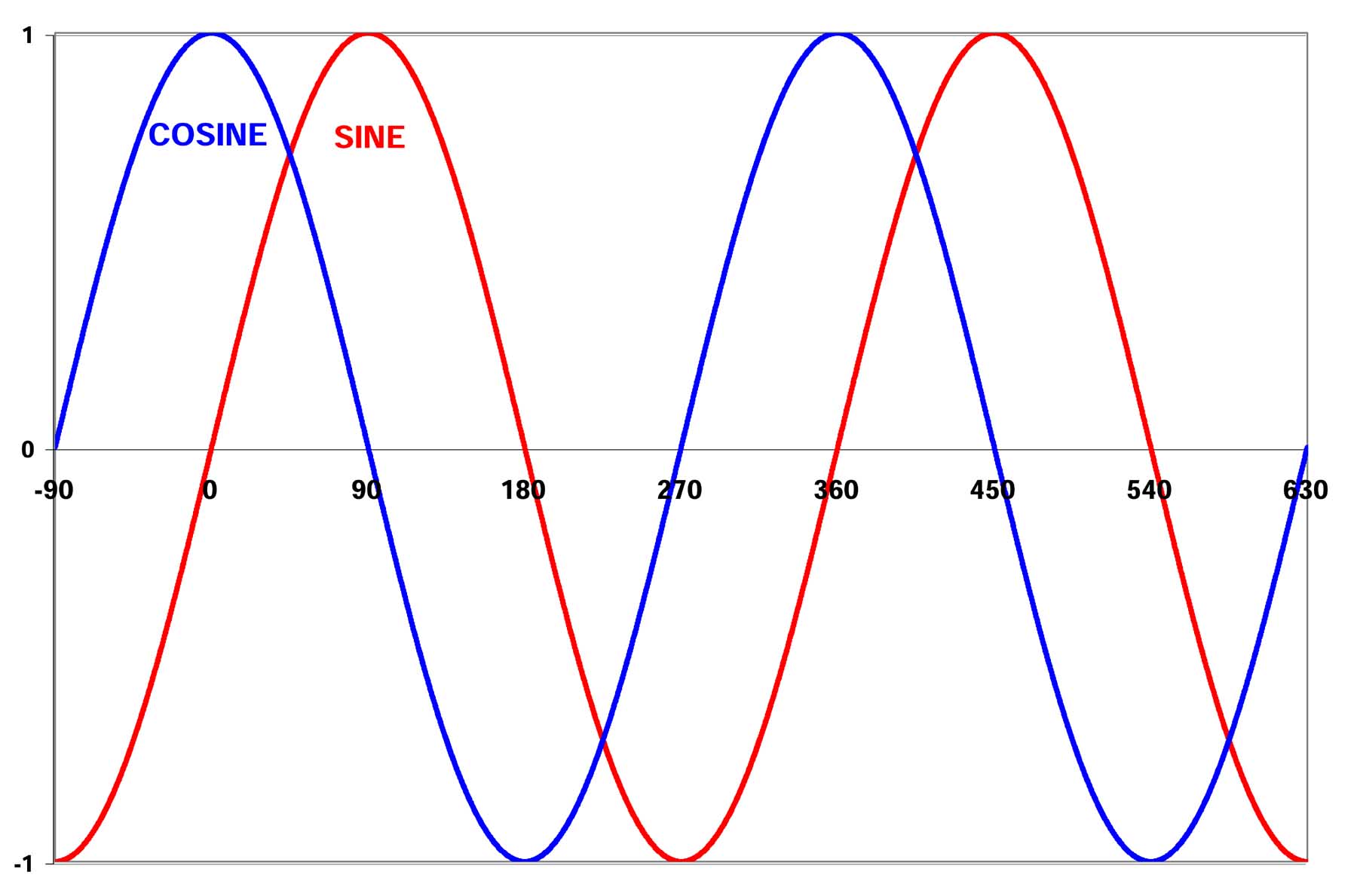
For more compact discussion call the Base Angle, (the angle between c and a), the angle B. Call the angle between
c and the other short side A where B = (90-A).
From the symmetry seen in the above graph, it should be clear that the sine of B is the cosine of A and
vice-versa and thus we can write the identity that sin(A) = cos(90-A).
Other clear relationships are that sin(-A) = -sin(A) and that cos(-A) = cos(A).
These relationships are valid not only for angles of the given triangles but also
for
all planar triangles.
If the hypotenuse of one of our family of triangles were scaled, up or down, from
unity to some value r, its sides would remain in the original proportion but would
then have lengths r times cos(A) and r times sin(A).
Thus given the hypotenuse
r and one of the angles G, (A or B), the length of the short side adjacent to that
angle can be found as: r*cos(G) and the other as: r*sin(G).
(The * is used in Excel2000 to signify the operation
of multiplication.)
Similarly the length of a short side and one of the angles A or B will allow the
hypotenuse to be determined.
Returning again to our family of rt triangles, and
noting the equality of side lengths to sine and cosine values, we conclude
that:
sin(A)2
+ cos(A)2
= 1.
If the triangle were scaled this relationship would not be affected as the
r2's would factor out of both sides
of the equation.
This identity is often used to find cos(X) given sin(X) and vice-versa.
Next
The spreadsheet is employed to discover a close approximation to the ratio of a
circle's circumference to its diameter.