Chapter 1
The Ratio of the Circumference of a Circle to its Diameter
This topic will be investigated using
a spreadsheet.
Some viewers may welcome the review of spreadsheet concepts that is available next;
others will skip over it.
Review: A spreadsheet consists of rows and columns of cells. Microsoft's
Excel identifies rows by numbers, 1, 2, 3, .... . Columns
are named alphabetically, A, B, C, ........... . Cells are identified by their
row and column position.
Briefly, each cell may be empty, contain text, contain explicit numeric values,
or contain a result from the operations described in an expression.
An arithmetic expression is indicated when the leftmost character position of a cell's content
is an equals sign, =.
Valid text that follows the equals sign is treated as an expression that describes
the operations to be carried out in the sheet to form a result that is placed in
the cell. Clicking the cell will provide its expression on the sheet's editing
bar.
Expressions will often refer to and employ results contained in other cells.
As an example of explicit content, cell J21 could contain the fixed value
0.1.
For an expression, cell I24 could contain: =I23+J21.
This means that I24 will display the value that is the sum of the value to be found
in cell I23 and the fixed value displayed in J21.
When an expression is copied from a given row and column to another location its
cell addresses will normally change relatively unless a $ symbol has been inserted
in front of a column or row address, e.g., the expression =I23 + J$21, if copied
in the Ith column from row 24 to row 25 would become =I24 +J$21. This behaviour makes constructing further rows and columns for successive steps of a calculation
quite easy to accomplish. |
An easy
arc of a circle to employ is the region: x from 0 to 1 with y from √2 to 1 and
with x, y constrained by x
2+y
2
= 2. This is a 45
o arc comprising
1/8 of the circumference of a circle of radius √2. The diameter of the circle is
2√2.
The length of this arc can be approximated by summing the lengths of contiguous
chords that are placed along the whole of the arc. The example following shows
four such chords.
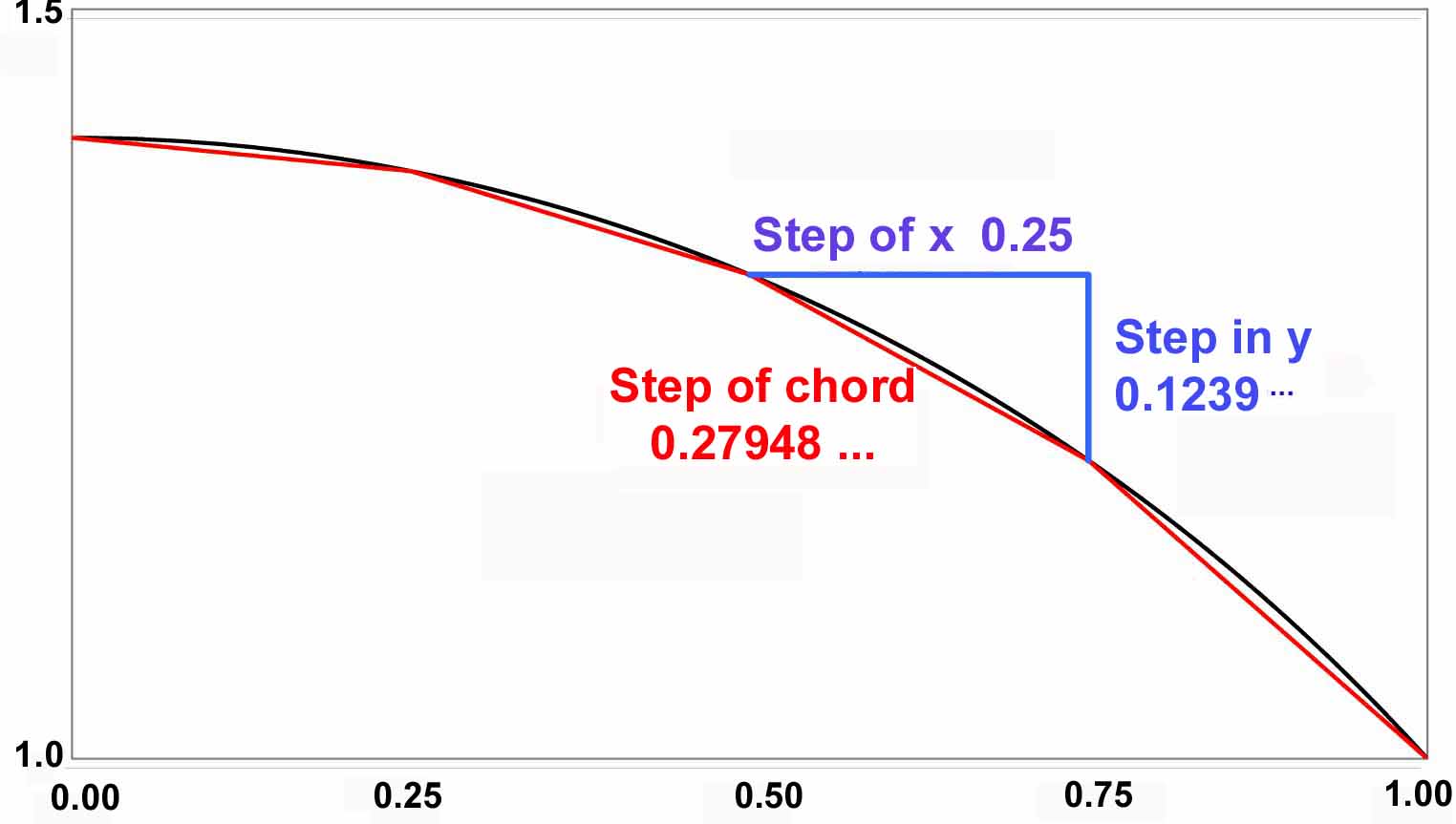
In the example, x increases in steps of ∆x = 0.25. For each step of x, y decreases by an amount ∆y that has to be determined for each
step in x. Given x, y and ∆x, the change
in y can be found using the constraint equation,
x2+y
2 = 2.
That is: (y+∆y)
2
= 2 -(x+∆x)
2
.
|
Hence: ∆y = √
|
2 - (x + ∆x)2
|
- y |
From the example it appears that the sum of these chords
will always
be a little less than the arc but the difference between the two would be smaller
if ∆x were smaller.
Further, one would presume that the difference could be made as small as we wish by choosing
∆x ever smaller.
As ∆x and
∆y
form the sides of a rt triangle, ∆Arc,
the length of a
chord increment, is given by:
For an initial run, using a spreadsheet, choose steps,
∆x = 0.1. (The sum of such steps forms x.)
Then determine the y values from
the x values using the constraint equation.
∆y is then found
as the change in the y value resulting from the just previous step of x. (
∆y
= current y - previous y)
∆Arc is then calculated from ∆x
and
∆y.
Finally the values of ∆Arc are accumulated to approximate the length
of the 45
o arc.
Initial and final steps and their results for this trial run, and
examples employing yet smaller values
for
∆x
,
may be seen by placing your mouse pointer over the
∆x
values given in the table that follows:

The table contains a row of initial values of the variables followed by a row of outlined
cells. The cells below an outlined cell all contain the same, relative, expression as
that contained in the outlined cell of that column.
The expressions, employing the addressing appropriate for the step size
∆x =
0.1, the initial run, can be viewed by clicking the (column, row) addresses following:
With step size 0.1 the ratio of circumference to diameter found is 3.14075994. With 0.0001 it is
3.14159265276.
The implication is that the exact ratio must be a bit larger
than either of these values and closer to the second value than to the first.