The top right quadrant of a circle
consists of an
upper 45
o arc and lower
45
o arc. Choose a circle with radius
√2.
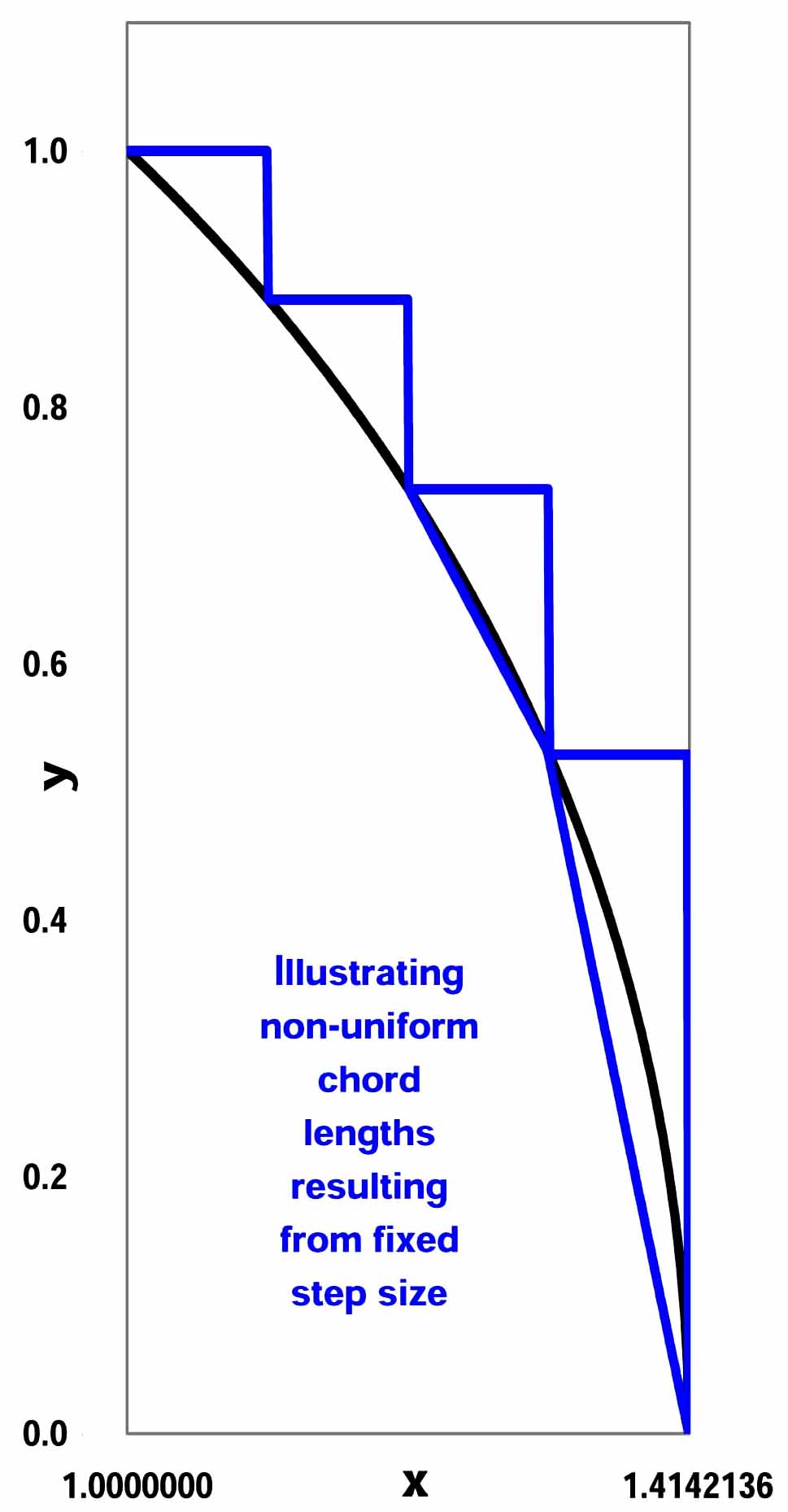
The lower arc is shown below at left with four uniform steps in
the x
direction.
A chord is constructed
for each step.
Note the increasing separation
between the chord and
the arc as the chord
lengthens.
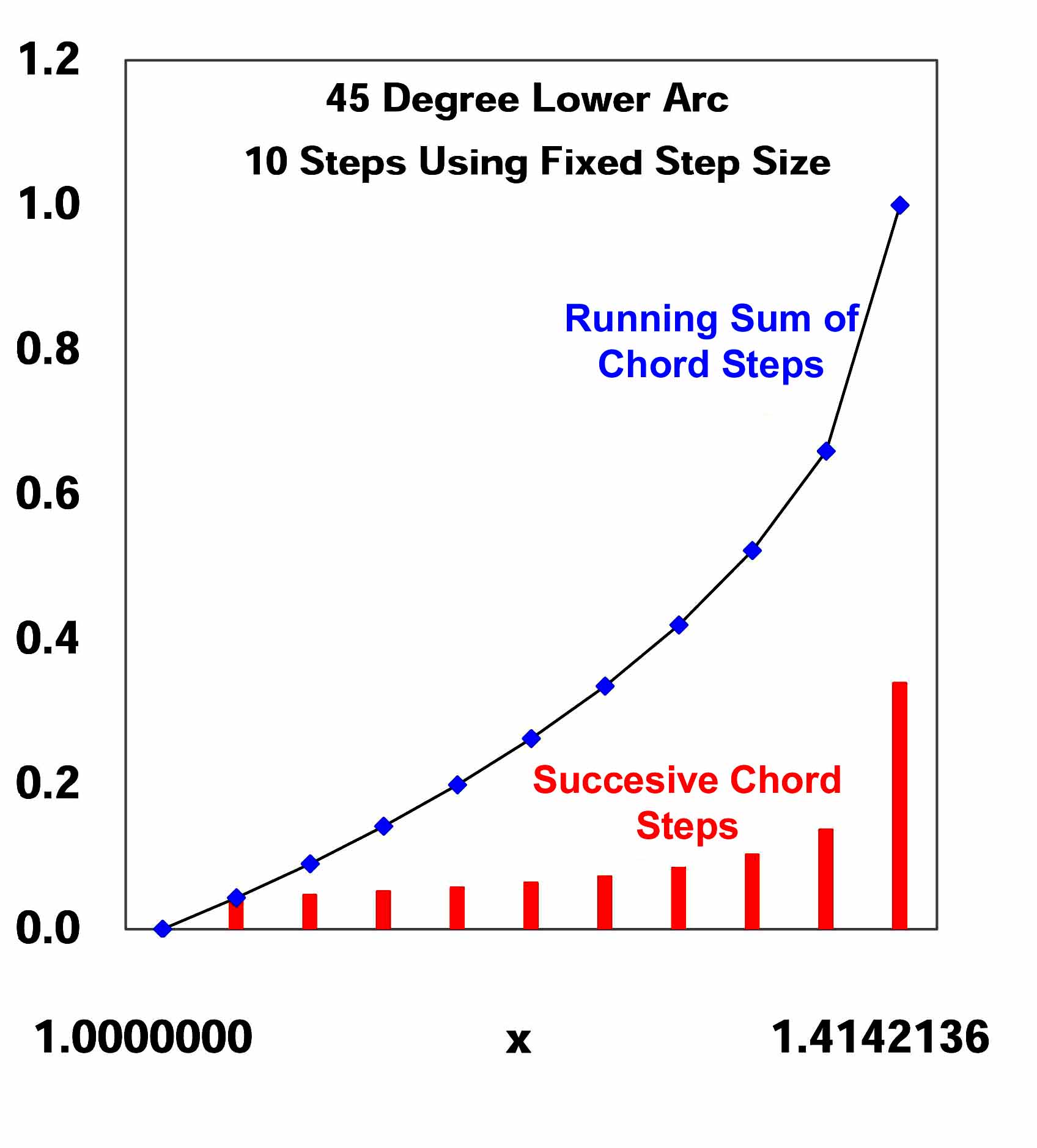
Shown lower, for ten equal steps in x, is the
sequence of chord step values, in
red, and their sum.
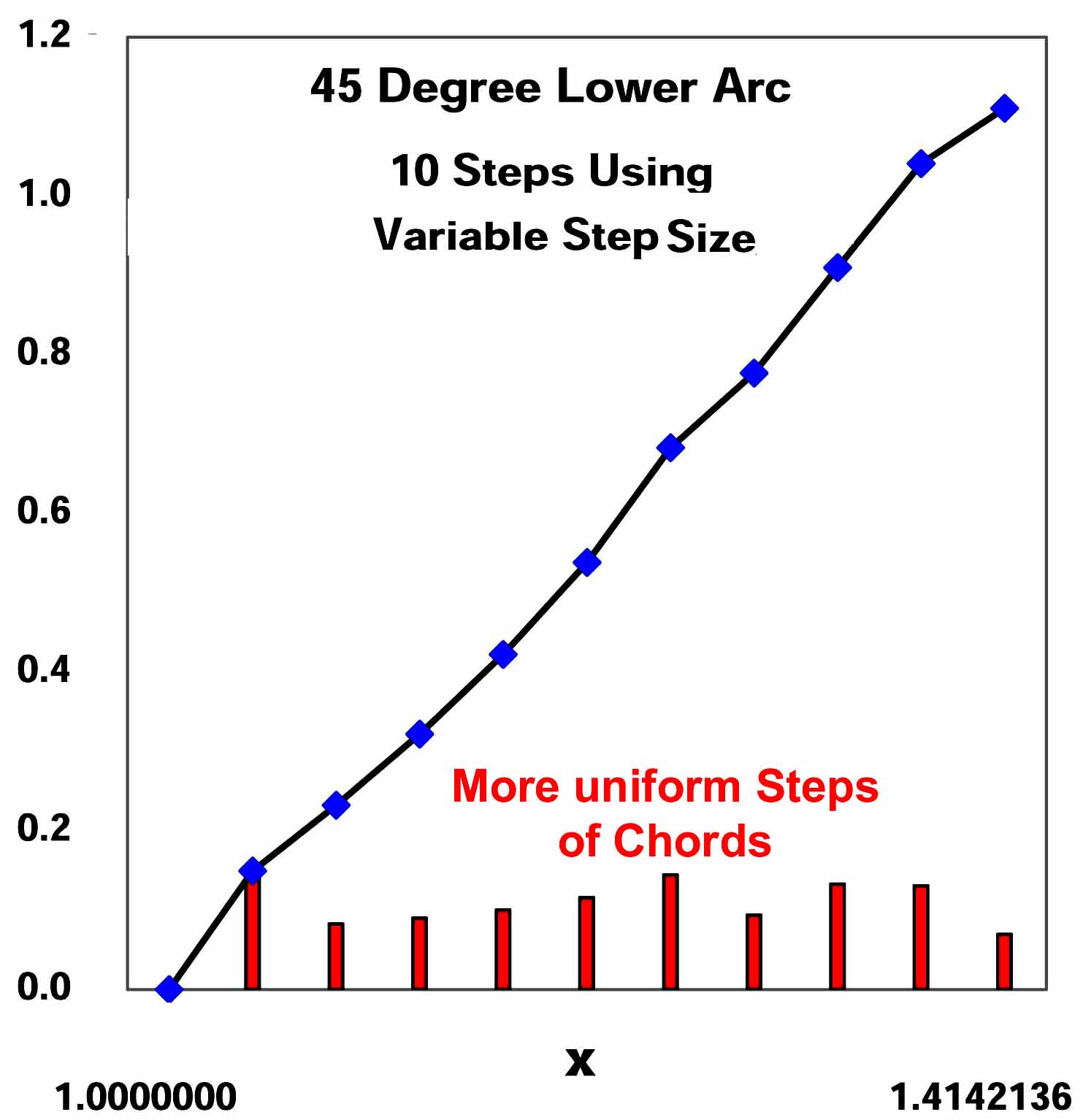
At left is shown the effect of using variable size
steps in x to create more uniform steps in the chord sizes, again using just ten steps.
Ideally, the increasing sum would show as a straight
line.
The final step is smaller because the sum of the preceding chords
came close to the end of the 45
o arc.
The method employed for adjusting step size used a "set"
value of √2 for chord length. If,
in a previous step,
the set chord length was
exceeded, then the step in x was halved.
If x
was about to exceed √2, then the final step in x was
adjusted to just reach √2 at the
end of the 45
o
arc.
This simple
procedure was chosen because it was presumed that, for this problem, step
size in x would
not need
to be increased.
The estimated ratios of the circumference of a circle to its diameter reached by
the two
methods are
distinctly
different. With
10 uniform steps in x, the estimate was 2.82842.. . With ten non-uniform
steps it was 3.14064.. .
From our earlier work, using 10,000 uniform steps, we know that the ratio must be greater
than
3.1415926527.
There are many possible algorithms to adjust step size but extra calculation is required
to
decide to
change step size.
Highly accurate adjustment might require an amount of calculation greater than that
required
to
achieve the
same accuracy by simply reducing step size.
The spreadsheet cells for adaptive step size follow.
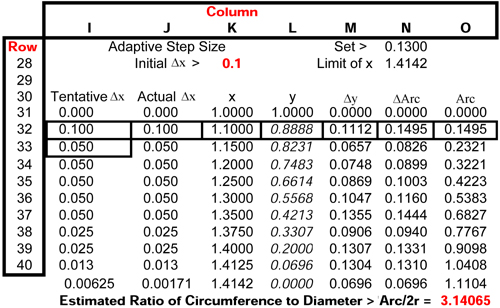
Relevant expressions can be viewed by clicking the (column, row)
addresses following:
|
I32 |
J32 |
K32 |
L32 |
M32 |
N32 |
O32 |
I33 |
More will be said in
subsequent topics about choice of step size.
Next
In this topic we developed a lower bound to the ratio of circumference to diameter.
The
next topic deals both lower and upper bounds and with the ratio of a circle's
area to the square of its radius.