Chapter 6
Application of the Atmospheric Model to Projectiles Part B
Modeling a Grenade or Paintball Launcher.
Many paintball launchers imitate the M203 Grenade Launcher. A U.S. army description of the M203 follows:

Find more detail on the Launcher specifications at M203
.
See a cartridge for M203 for the following cartridge
image.
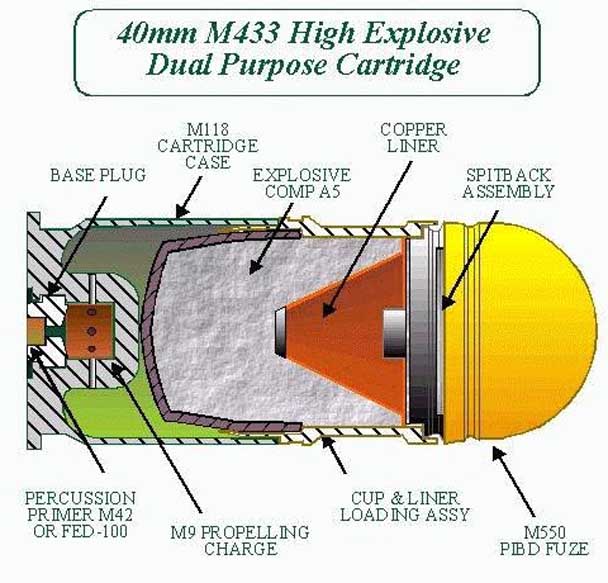
The lethal range of the grenade is about 5 metres. The nominal maximum target range
of the M203 for area targets is 350 metres; for point targets it is 150 metres.
The minimum safe range is 31 metres.
The launcher has a maximum range of 400 metres. The shell achieves a muzzle velocity
of 74.7 metres per second. The cartridge weight is 0.23 kg. The shell will weigh
some fraction of this. We suck a thumb and say 0.16 kg. The radius of the cartridge
is 0.02 metres.
All that is needed now for a model is the drag coefficient. We
obtained this by guessing a value and then adjusting it in the web based calculator version
of the 2D spreadsheet
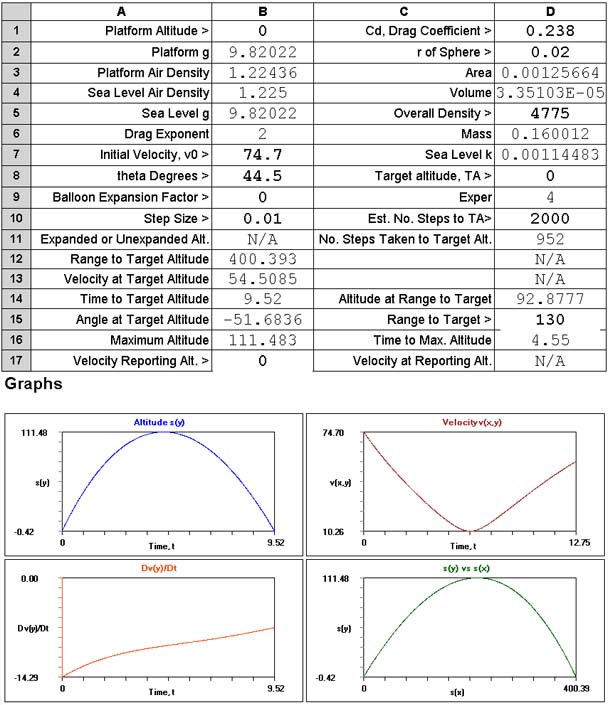
until a maximum sea level range of 400.393 metres was achieved with a drag coefficient
of 0.238. This was found at an elevation angle of 44.5 degrees. A
density of 4775 assures the desired sea level weight of the shell. The result for sea
level maximum range, using the web-based 2D Calculator,
described further and available subsequently, is
shown next.
The web-based calculator emulates the spreadsheet
calculator and is available to the viewer at the end of
this topic.
Note that an artillery spotter has been at work to report the range at which the
shell reached the target altitude, shell velocity at the target, the time taken
and the angle between the shell and target. Additionally the spotter noted the maximum
altitude and the time taken to achieve it.
Maximum Elevation
At an altitude of 500 metres, for both platform and target, a range of ~ 31
metres is achieved using an elevation angle of 88.2 degrees. The time to target is a little
over 13 seconds. Use of a higher elevation will land the shell closer to the launch point
and could adversely affect
the grenadier.
Range for Point Targets - Moving Targets
At altitudes of 500 metres a range of ~ 150 metres is achieved with an elevation
of ~80.5 degrees. The time taken to reach the target is a little more than 13 seconds.
In 13 seconds, a target moving at a speed of 10 km per hour will change position
by over 36 metres.
Unless the grenadier employs an appropriate lead, a moving target could
be out of harm's way by the time the grenade arrives.
The calculator does not offer a facility for employing lead. Lead is the responsibility
of the grenadier and is presumed to be provided correctly.
The Calculator, Its Assumption and Usage
The calculator computes the range to target altitude on the assumption that impact
occurs with the grenade arriving from above.
For example, assume a target is well back from the edge a cliff at an altitude above
the launch platform. The calculator presumes that the target is reached from
above by a lobbing shot and not by a shot from below that has penetrated the cliff
face.
To shoot into a cliff face, wall or tank an elevation angle must be chosen such
that the projectile reaches the Range to Target at an appropriate altitude. It could
overshoot the target or undershoot the target. The calculator has no information
on the terrain between the platform and the target and presumes that it is atmosphere.
To assist the grenadier with this class of target, the calculator, spotter, reports the altitude
of the projectile at the time Range to Target is reached. If
too high, lower
the elevation, if too low raise it. If the Range to Target
is not reached, the
calculator will return, "Range not Reached". There will not be a report of "On Target!!"
as the calculator is unaware of the range of elevation occupied by the target.
For an example of this type of target, assume that the platform is at an altitude
of 500 metres, there is a 30 metre high vertical cliff at a horizontal distance
of 127 metres. Aircraft spotters report a tank at 3 metres back from the edge
of the cliff. A shell hitting the cliff face about 3 metres below its
edge might well crumble enough of the cliff to drop the tank. Let's try that.
Between consulting our artillery tables and a couple of trial shots we do it, see
next.
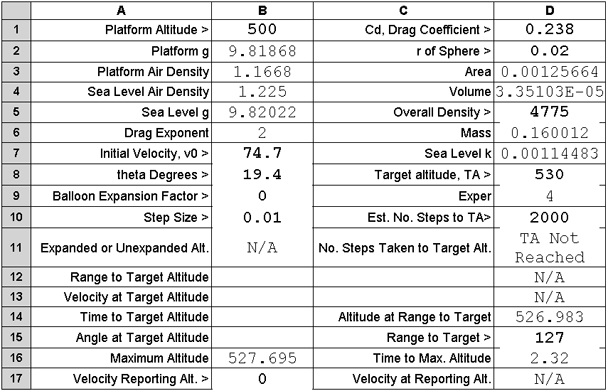
With an elevation of 19.4 degrees the altitude reached by the shell at the cliff
face, cell D14, is seen by the spotter to be about ~3 metres below the top of the cliff.
The grenade should explode there and may weaken the cliff sufficiently for the tank
to fall to its base. Another way to hit the tank is to drop a grenade on it
from above with a lobbing shot. See next.
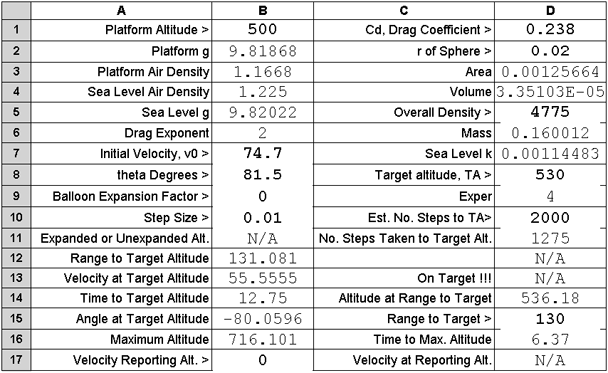
We set Range to Target at 130 metres. With an elevation of 81.5 degrees, the shell
fell ~ 1 metre long. The spotter sent the message OnTarget!!, row 13 column C, because
the grenade fell within 5 metres of Range to target. A grenade falling within
5 metres should damage or disable a tank and would be fatal to personnel in the open.
What if the positions of platform and target were exchanged? The grenadier
might again try a lobbing shot or move close to the cliff edge to make a clear shot.
Presuming the latter, the horizontal distance to the target will be 127 metres.
Using an elevation of - 7.0 degrees the shot falls short of the tank as shown next.
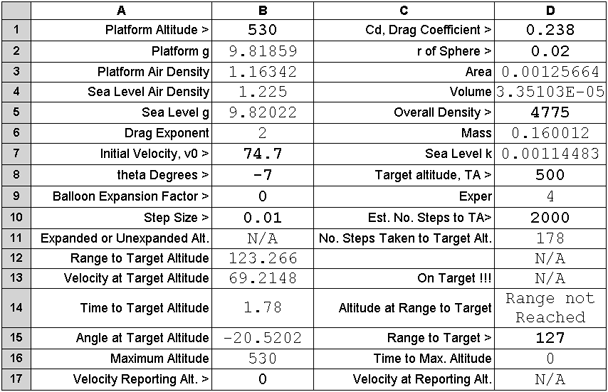
The grenade reached the target altitude ~ 3.7 m short of 127 metres. Close enough to be declared
On Target!!, but possibly not close enough to destroy a tank. Try again but
use an elevation of -6.0 degrees as is shown next.
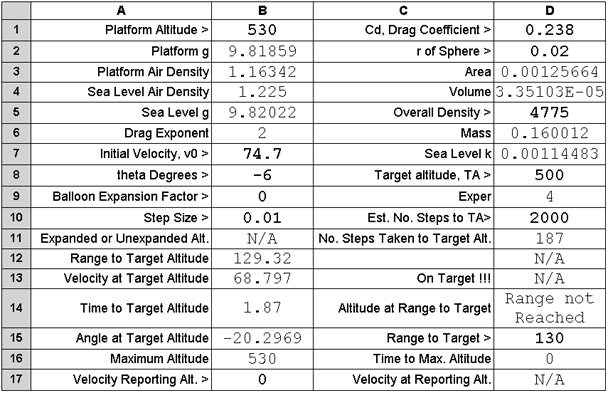
This time the grenade reaches Range to Target within a metre and should score on a tank.
Calculator Summary
The calculator can be used to hone the skills of a paint ball enthusiast, to polish
ballooning skills, and to increase the depth of a student's understanding of the environment
in which he lives.
Click here to access this 2D Calculator. (The
2D Calculator is also available on the top row of Navigation tabs.)
Remember that the calculator takes into account atmospheric resistance that is proportional
to the square of velocity, variation in gravity with altitude, atmospheric
density for altitudes from -5.0 km to 1000 km and the effect of atmospheric buoyancy.