Chapter 6
Application of the Atmospheric Model to Ballooning Part B
Aspects of Pressurized Gas Balloons
Most recently, restraint is built into
the fabric of the balloon to reduce the likelihood of bursting. Exterior netting has been employed.
There is a 1976 (PDF) report
on this subject,
BT-1044.09,
"The First Year of the ATMOSAT Project",
that may be downloaded from The Goddard Library
describing such balloons. The abstract follows:

The pressure balloon will often be partially filled with lifting gas at ground level and
then ascend until fully expanded and continue ascending until its overall density matches that of the surrounding atmosphere. In the later segment of the ascent
the gas pressure will rise.
Such balloons have a limit to the pressure that they are able to withstand without
bursting but within that upper limit the balloon will float at a more or less stable
altitude. At times some gas may need to be vented to avoid the threat of bursting.
Having reached a stable altitude with a pressurized balloon it is possible, by venting
a small amount of gas, to descend and float at stable altitudes that are above the
altitude at which full expansion occurred.
Venting enough gas to drop below the full expansion altitude will return the balloon
to earth unless enough ballast is released to allow the balloon to again rise and
fully
expand. Release of a smaller amount of ballast will slow the
rate of descent.
Modeling the Ascent and Descent of a Pressurized Balloon
The Web-based 2D Calculator version of the spreadsheet, available from the upper
row of navigation tabs is used for the modeling.
The spreadsheet Parameter Table follows:
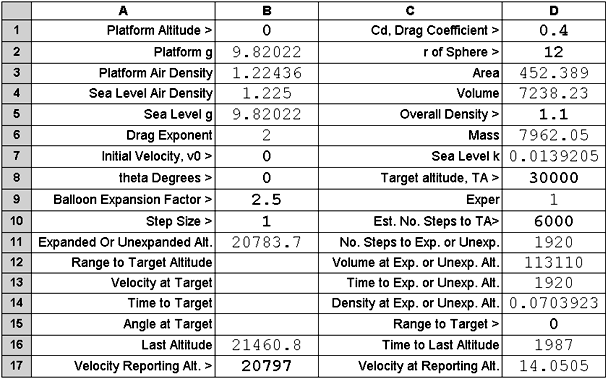
The partially filled balloon and payload had a density of 1.1 at its sea level launch
site. This is less than the surrounding atmospheric density of 1.22... and thus
the balloon rises into the air.
The expansion factor provided to the macro is 2.5. The balloon reaches full expansion
to a radius of 30 metres
about 32 minutes later at an altitude of ~20,784 metres.
It continues to rise for
just over a minute, stopping at its float altitude of ~ 21,461 metres. At
float altitude the balloon and payload have a density equal to that of the
surrounding atmosphere, ~0.07039.
Graphs of the altitude and velocity of the balloon ascent versus time are shown next.
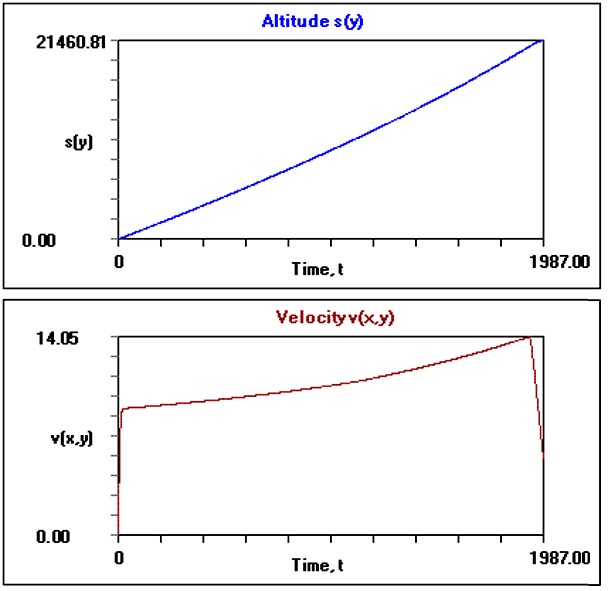
The velocity of ascent over time is the more interesting.
At launch, the balloon's rate of rise rapidly reaches ~9.0 metres per second, it
then
speeds up reaching ~ 14.0 metres per second at full expansion. Its rate
then falls rapidly
as float altitude is approached.
The velocity does not drop to zero on reaching float altitude. The kinetic energy
of the balloon will force it to overshoot that altitude. Once above float altitude
the balloon looses buoyancy to the point where gravity will accelerate it back down
through float altitude, having lost a little of its energy to atmospheric friction.
The balloon will again become buoyant and soon reverse direction to move upward
through float altitude again.
This up then down cycle repeats with the maximum excursion from float altitude slowly
diminishing with each cycle.
Rather than continue calculating
through a great many cycles looking for convergence to the float altitude,
the macro is designed to stop calculating at the calculation step when
float altitude is first exceeded.
Of course the calculated behaviour is not an accurate representation. A great many influences
such as atmospheric temperature, radiant energy from the sun, stretch in the balloon
fabric, condensing of residual moisture in the lift gas, etc., have been ignored. Nonetheless, the calculated behaviour should bear a resemblance to the actual behaviour of such a balloon.
Float Altitude
To test the effect of floating, supply the spreadsheet with the platform
altitude of 21,465 metres, 10 metres above float altitude. Set the balloon radius to
30 metres.
No expansion or contraction relative to this platform altitude is wanted, therefore set the balloon
expansion factor to zero. The macro then ignores expansion.
The overall density of a pressurized balloon does not change at altitudes above the fully expanded
altitude. Thus employ the density that was achieved at that altitude.
On running the macro the results are:
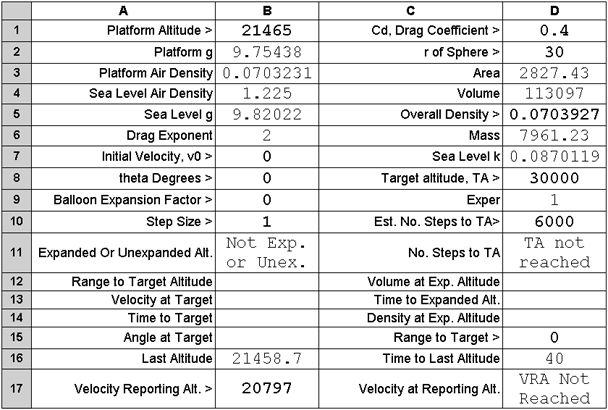
Note that the balloon falls to approximately its previous float altitude. The
small difference is largely due to the finite step size of 1 second.
We could equally well have lowered the platform altitude to 10 metres below float
altitude and the balloon would have ascended to approximately float altitude.
Venting some Lift Gas
The effect of venting a little of the lifting gas will be to increase the overall
density a little. One has to be careful about how much, else the balloon will
descend to earth. This is illustrated next.
On the spreadsheet, increase overall density by 0.01.
Since we expect with this
change that the balloon will no longer be fully expanded, set the balloon expansion ratio to 0.4.
Set the target
altitude to zero. This will cause calculation to stop at the first
step at which the altitude is less than 0.0.
Change the velocity reporting altitude
to 0.0 metres and run the macro.
That case is shown next:
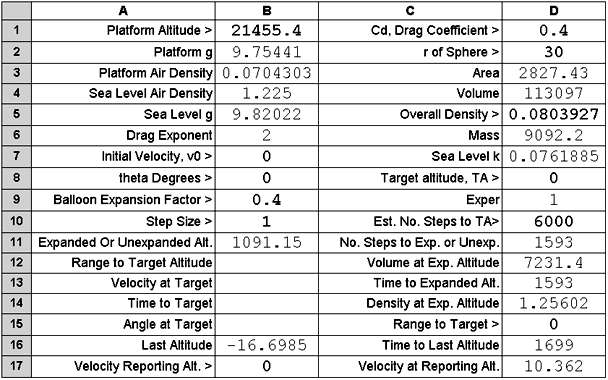
From the volume seen in D13, the balloon deflated to just under its launch radius at an altitude of ~ 1091 metres.
From the step-by-step table, not shown, the velocity at that altitude was ~10.91
metres per second.
The balloon lands at a velocity of ~10.36 metres per second, e.g. the payload hits the earth at ~37 km. per hour or ~ 23 miles per hour!
An amount of ballast could have been cast out before reaching the ground to reduce this speed.
Less lift gas
vented at the peak altitude would have resulted in a lower speed at earth impact.
Reaching a Lower Float Altitude
Venting a still smaller amount of lift gas at the 21,455-metre altitude, an amount limited
so as to retain full expansion, will result in a lower float altitude.
Try adding half as much, 0.005, to the overall density and set the expansion factor at 0.0 as we plan on remaining
in the full expansion altitude range.
See the result next.